 Commons Nabla
Commons Nabla
Nabla is an algorithmic differentiator for mathematical functions.
Just like the mathematical Nabla operator transforms a function into its differential, the Nabla library transforms an existing java object implementing a function
double value(double) { ... }value like the original one also computes
its derivative. The created object is built by applying the
classical exact differentiation rules to the function
underlying expressions. There are no approximations
and no step sizes.
This approach has the following benefits:
The derivative instance remains tightly bound to the base instance (which is refered to as its primitive) throughout its lifetime. If the internal state of the primitive instance is mutated after Nabla has performed the transformation, the already created derivative instance which is bound to its primitive will use this mutated state for its computation automatically.
The following example should explain better what Nabla can do.
Let's consider a simple problem: we want to find the maximal value of a function:
f(t) = (6-t)/3 + cos(4t-4) e-0.9t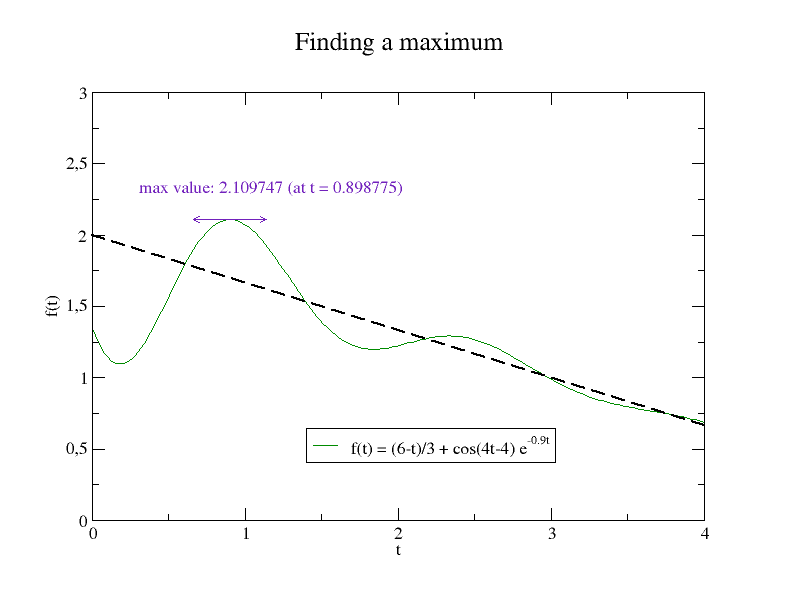
The maximal value is reached when the first derivative of
the function is equal to zero. So we need to compute the
first derivative f'(t) and find its
roots. Nabla will help in the first part:
computing f'(t).
In order to compute f'(t). We start by implementing the
function f(t):
UnivariateFunction function = new UnivariateFunction() {
public double value(double t) {
return (6 - t) / 3 + Math.cos(4 * t - 4) * Math.exp(-0.9 * t);
}
};
We use the Nabla algorithmic differentiator to differentiate our function and obtain an object implementing the derivative:
UnivariateFunctionDifferentiator differentiator = new ForwardModeDifferentiator();
final UnivariateDifferentiableFunction derivative = differentiator.differentiate(function);
The derivative object implements the Apache Commons Math UnivariateDifferentiableFunction
interface which means it provides a method value which is an enhanced
version of the value method of the original function object:
it computes both the value and the partial derivatives of the function.
We can therefore find the maximal value by calling a solver on the derivative. As functions passed to any Apache Commons Math solvers must implement a specific interface: UnivariateFunction. In order to comply with this interface, we wrap the derivative instance:
UnivariateFunction wrappedDerivative = new UnivariateFunction() {
public double value(double x) {
// the VALUE of this new function is the DERIVATIVE of the original function
DerivativeStructure t = new DerivativeStructure(1, 1, 0, x);
return derivative.value(t).getPartialDerivative(1);
}
};
The final step is to call a solver on the derivative, as the roots of the derivative are the local extremum of the original function. In this example, we will use the bracketing nth order Brent solver from the Apache Commons Math library:
UnivariateSolver solver = new BracketingNthOrderBrentSolver(1.0e-6, 5);
double tMax = solver.solve(100, wrappedDerivative, 0.5, 1.5);
double yMax = derivative.value(new DerivativeStructure(1, 1, 0, tMax)).getValue();
System.out.println("max value = " + yMax + ", at t = " + tMax +
" (" + solver.getEvaluations() + " evaluations)");
We get the following result:
max value = 2.1097470218140533, at t = 0.8987751646846582 (11 evaluations)
The example above shows that Nabla creates an object that computes both the value and the derivative of a function, given only an instance of a class that computes the primitive function. Despite we had the source code available in this case, it was not used: transformation is done at runtime using only an instance of the primitive function. We can also observe that there is no configuration at all: the algorithmic differentiator is built using a no-argument constructor and the differentiation method has only the primitive object as a parameter.
We could also use the derivative object to compute both the value and the first derivative of our function at any point:
for (double t = 0.0; t < 1.0; t += 0.01) {
DerivativeStructure y = derivative.value(new DerivativeStructure(1, 1, 0, t));
System.out.println(t + " " + y.getValue() + " " + y.getPartialDerivative(1));
}
Basically, Nabla works by:
The main drawback of this approach is that functions that call native code cannot be handled. For these functions, a fallback method is to uses finite differences using the Apache Commons Math library. This fallback method does not have the same advantages as the previous one: it needs configuration (number of points and step size), it is not exact, it is more computation intensive and it cannot be used too close to domain boundaries.