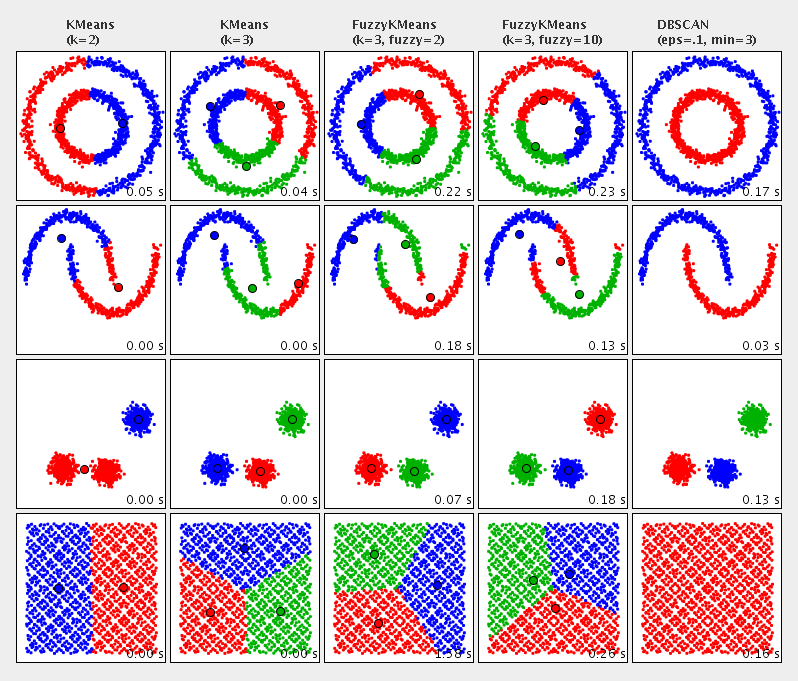
16 Machine Learning16.1 OverviewMachine learning support in commons-math currently provides operations to cluster data sets based on a distance measure. 16.2 Clustering algorithms and distance measuresThe Clusterer class represents a clustering algorithm. The following algorithms are available:
An comparison of the available clustering algorithms: 16.3 Distance measuresEach clustering algorithm requires a distance measure to determine the distance between two points (either data points or cluster centers). The following distance measures are available: 16.3 Example
Here is an example of a clustering execution. Let us assume we have a set of locations from our domain model,
where each location has a method The cluster algorithms expect a list of Clusterable as input. Typically, we don't want to pollute our domain objects with interfaces from helper APIs. Hence, we first create a wrapper object:
// wrapper class
public static class LocationWrapper implements Clusterable {
private double[] points;
private Location location;
public LocationWrapper(Location location) {
this.location = location;
this.points = new double[] { location.getX(), location.getY() }
}
public Location getLocation() {
return location;
}
public double[] getPoint() {
return points;
}
}
// we have a list of our locations we want to cluster. create a
List<Location> locations = ...;
List<LocationWrapper> clusterInput = new ArrayList<LocationWrapper>(locations.size());
for (Location location : locations)
clusterInput.add(new LocationWrapper(location));
// initialize a new clustering algorithm.
// we use KMeans++ with 10 clusters and 10000 iterations maximum.
// we did not specify a distance measure; the default (euclidean distance) is used.
KMeansPlusPlusClusterer<LocationWrapper> clusterer = new KMeansPlusPlusClusterer<LocationWrapper>(10, 10000);
List<CentroidCluster<LocationWrapper>> clusterResults = clusterer.cluster(clusterInput);
// output the clusters
for (int i=0; i<clusterResults.size(); i++) {
System.out.println("Cluster " + i);
for (LocationWrapper locationWrapper : clusterResults.get(i).getPoints())
System.out.println(locationWrapper.getLocation());
System.out.println();
}
|